【愛媛県立入試問題】第１６回ピントゼミナール！！

第１６回ピントゼミナール

本日は、「資料の活用」の分野から抜粋しました。

実を言うと、ゆとり世代と呼ばれる我々世代は、この分野を中学校で学んでおりません。

私はエクセルの基本を学んでいる時に学びましたが、そのまま出会うことがない人も多い分野でしょう。

ぜひ同世代の方々は、ここで基本を学んでみてくださいませ。

ゼミ長メッセージでは、校則のお話。

中学時代、生徒会長として校則を変えた過去があります。

でも2つ目以降の校則変更は、「そんなに一気に変えるべきではない」と一蹴されました。

確か、マフラーに関する校則だったかな。

それでも「変えられた」のは自信になったし、今でもそのスピリッツは自分の中にあります。

変わっていくことができるのは個人だけでなく、組織にとってもメリットだと思うよ。

「変わる」ことだけが大事なわけじゃなく、「変わっていけること」が大事。

数学〜資料を読み解こう〜

基本を学ぼう

次の資料は、ある中学校の生徒7人の懸垂の回数です。このとき次の問いに答えよう。

6 2 4 10 2 0 11

(１) 中央値を求めよう

(２) 平均値を求めよう

【答え】

（１） 4（回）

（２） 5（回）

【解き方】

資料の特徴を見つけるために、代表的な3つの値（代表値）を覚えて置くといいよ！

中央値：資料の値を大きさの順に並べたときの中央の値のこと。資料が偶数個のときは、中央に並ぶ2つの値の平均をとるよ！

平均値：資料の個々の値の合計/資料の個数　の式で求められる値のこと。

最頻値：資料の値の中で、最も多く現れる値のこと

（１） 中央値を求めたいので、資料の値を小さい順に並べると

0 2 2 4 6 10 11

となるね。その真ん中に位置する値は、４だね！

（２）平均値を求めたいので、資料の個々の値の合計/資料の個数に値を当てはめていこう。

資料の個々の値の合計は、6 2 4 10 2 0 11を足した数だね。

6+2+4+10+2+0+11=35

資料の個数は、7個だね。

資料の値が０でも。資料の個数は１になるよ！

よって平均値＝35/7=5となるよ。

問題にチャレンジ

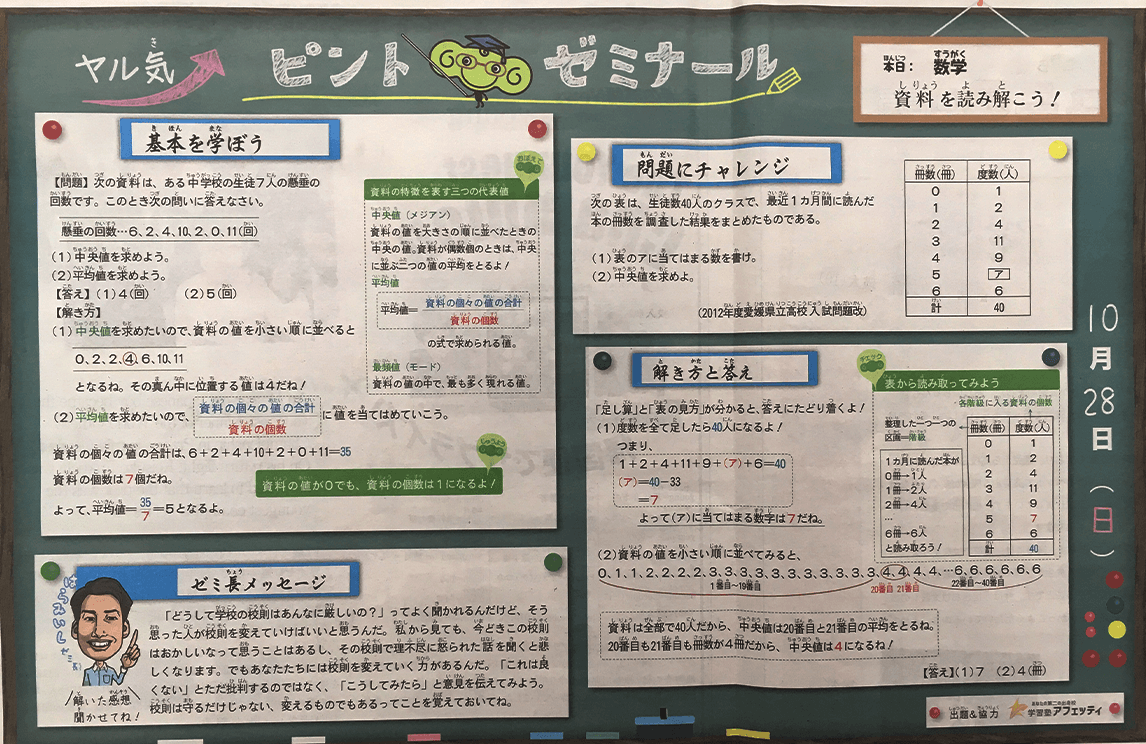
次の表は、生徒数40名のクラスで、最近一か月間の間に読んだ本の冊数を調査した結果をまとめたものである。

（１） 表のアに当てはまる数を書け。

（２） 中央値を求めよ。

（2012年度愛媛県立入試問題改）

解き方

「足し算」と「表の見方」が分かると、答えにたどり着くよ！

（１） 生徒数を全て足したら40人になるよ！

つまり、

１＋２＋４＋１１＋９＋（ア）＋６＝４０

（ア）＝４０―３３

＝７

よって（ア）に当てはまる数字は７だね。

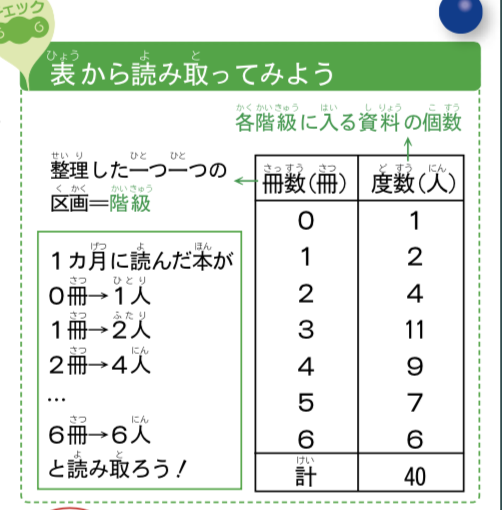
度数：各階級に入る資料の個数。

階級：整理した1つ1つの区間

（２） 資料の値を小さい順に並べてみると、

0,1,1,２,２,２,２,3,3,3,3,3,3,3,3,3,3,3,4,4,4,4,…,6,6,6,6,6,6

資料は全部で40人だから、中央値は20番目と21番目の平均をとるね。

20番目も21番目も冊数が4冊だから、中央値は4になるね！

【答え】

（１）７（２）４（冊）

ゼミ長メッセージ

「どうして学校の校則はあんなに厳しいの？」ってよく聞かれるんだけど、

そう思った人が校則を変えていけばいいと思うんだ。

私から見ても、今どきこの校則はおかしいなって思うことはあるし、

その校則で理不尽に怒られた話を聞くと悲しくなります。

でもあなたたちには校則を変えていく力があるんだ。

「これは良くない」とただ批判するのではなく、「こうしてみたら」と意見を伝えてみよう。

校則は守るだけじゃない、変えるものでもあるってことを覚えておいてね。