第31回ピントゼミナール
こんにちは、ゼミ長の孕石です。
本日は、数学です。
「並びかえは、なんパターン?」
というテーマです。
高校3年生・既卒のみなさん、センター試験お疲れ様でした。
アフェッティの塾生でセンター試験を使う方々は、
目標点突破いたしました!素晴らしい!
ただいま二次試験対策真っ最中です。
中学3年生は、私立入試が近づいてまいりました。
最後の仕上げを一緒に頑張りましょう!
基本を学ぼう
【問題】
1円玉と10円玉の2つの硬貨を同時に投げるとき、表と裏の出かたは何通りあるかな?
【答え】
4通り
【解き方】
考えられるすべての場合を数えるのに、樹形図や表をよく使うよ!
今回は、2通りのやり方で解いてみよう!
 【重要】樹形図をかいてみよう!
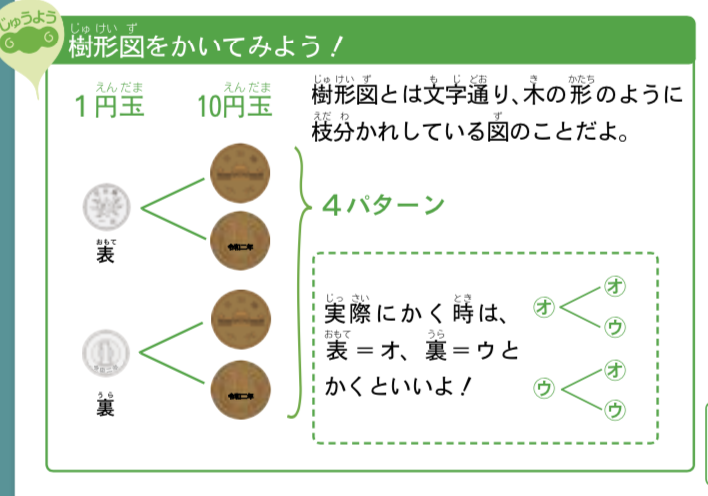
【重要】樹形図をかいてみよう!
樹形図とは文字通り、木の形のように枝分かれしている図のことだよ。
実際に描く時は、表=オ、裏=ウと書いてパターンを考えるんだ!
 【覚えて】表をかいてみよう!
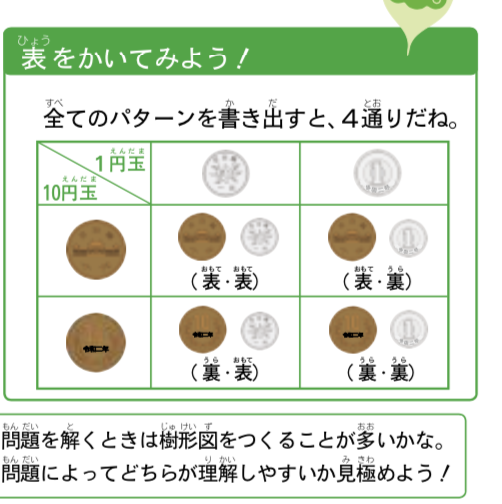
【覚えて】表をかいてみよう!
全てのパターンを書き出すと、4通りだね。
 【チェック】コインの裏表
【チェック】コインの裏表
「数字」が書かれている面が裏だよ。
「植物」や「建物」などが描かれている面が表だよ。
※5円玉は、例外
問題にチャレンジ
1,2,3,4の数字が1つずつ書かれた4枚のカードがある。この4枚のカードを横に並べて4けたの整数をつくるとき,
- 4けたの整数は、全部で何個つくることができるか。
- 2413は、小さい方から何番目か。
(2013年度愛媛県立入試問題改)
解き方
千の位から順に、百の位、十の位、一の位と数字を当てはめて考えていこう!
 【重要】(1)を、樹形図で考えよう!
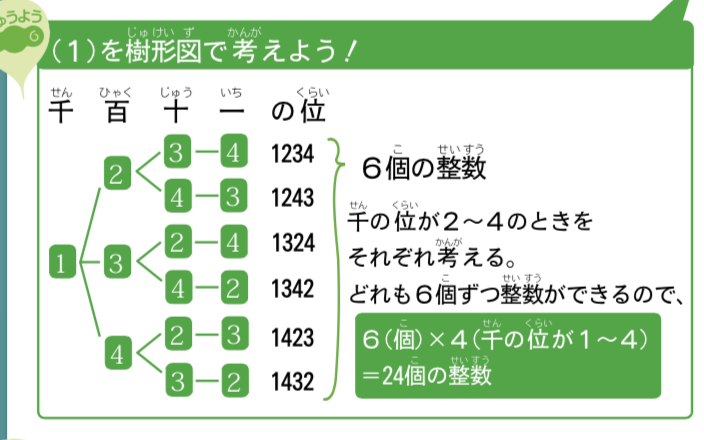
【重要】(1)を、樹形図で考えよう!
千の位が2〜4のときを
それぞれ考える。
どれも6個ずつ数ができるので、6(個)×4(千の位が1〜4)
=24個の数字
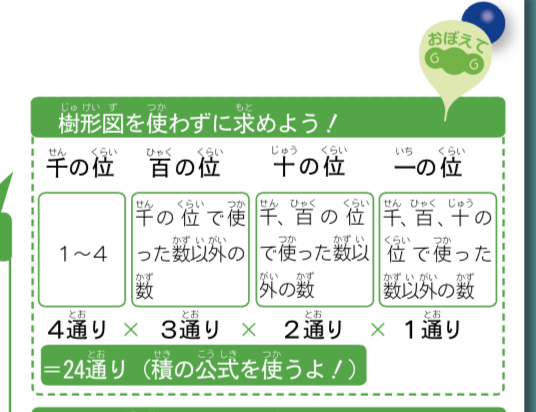
覚えて樹形図を使わずに求めよう!
=24通り (積の公式を使うよ!)
 チェック(2)は、小さい数から一つずつ書いてみよう!
チェック(2)は、小さい数から一つずつ書いてみよう!
1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413・・・と続いていくよ。
よって2413は、11番目になるね。
 【覚えて】全ての数字をかかずに求めよう!
【覚えて】全ての数字をかかずに求めよう!
(6通り+2通り+2通り)の次の数
つまり11番目だよ!
答え
(1)24(個) (2)11(番目)
ゼミ長メッセージ
「ガチャを引きまくっているのに、アタリが出ない!」ってよく言われるんだけど、
当たる確率が1%のガチャを100回引いても当たりが出るとは限らないよ。
100回に1回は必ず当たると信じて、時間とお金を無駄にしていないか心配だ。
他にも、さまざまな場面で確率と出くわすよ。そこで一つアドバイス。
◯◯(合格・就職・生存)率98%なんて聞いたら、まずは「確率の分母」を疑おう。
隅に小さく分母について書いてある場合もあるよ。
想像していた分母と異なるケースも少なくないんじゃないかな。
正しく読み解く力を鍛えていこうね!
投稿者プロフィール
-
学習塾アフェッティ塾長が主に書いているブログ。
一般社団法人多様な学び舎 代表理事
(フリースクールエルート理事長)
・愛媛県フリースクール等連絡協議会 代表
・NPO法人えひめ放課後協力機構 理事
・(愛媛県校内サポートルーム設置事業における)
不登校児童生徒等支援連絡協議会 委員
静岡県生まれ。
2012年4月、愛媛大学在学中に「対話」と「自立学習」メインの学習塾「学習塾アフェッティ」を開塾。
2019年4月、平日昼間の学校以外の学び場の重要性に気付き、「フリースクールエルート」を開所。
2015年、“未来を切り拓く29歳以下ニッポン代表”としてNHK(Eテレ)U29で特集される。
2017年より愛媛新聞ピントゼミナールゼミ長として「次代を生き抜くメッセージ」の連載中。
第1回(2018年)・第2回(2019年)松山市人間力大賞受賞。
2018年、第32回人間力大賞(青年版国民栄誉賞)会頭特別賞受賞。
2022年、フリースクールエルートでの取り組みが、『ルポ 誰が国語力を殺すのか』文藝春秋(石井光太著)に紹介される。
<<メディア実績>>
U29出演・おはよう四国・greenz・愛媛新聞・朝日新聞・南海放送・他多数
<<講演実績>>
愛媛大学・愛媛県教育研究協議会・市内小学校・四国若者1000人会議・まつやま経営プラザ・他多数
最新の投稿
 塾生ブログ2025.03.02塾に着いたら、ホワイトボードに。
塾生ブログ2025.03.02塾に着いたら、ホワイトボードに。 塾生ブログ2025.03.02とても辛い過去があったとしても、前向きな気持ちになれますように。
塾生ブログ2025.03.02とても辛い過去があったとしても、前向きな気持ちになれますように。 塾生ブログ2025.02.25「きっとうまくいく」と、私は私に言い聞かす。
塾生ブログ2025.02.25「きっとうまくいく」と、私は私に言い聞かす。 塾生ブログ2025.02.24感謝の思い、医師になってから。
塾生ブログ2025.02.24感謝の思い、医師になってから。




